
La receta clásica para el precio económicamente eficiente --- fijar el precio al costo marginal --- no es relevante para las tecnologías que presentan tipos de rendimientos crecientes a escala, grandes costos fijos, o economías de alcance que se encuentran en las industrias de telecomunicaciones y de información. El principio rector apropiado en estos contextos debe ser que la disposición marginal a pagar debe ser igual al costo marginal. Esta condición de la eficiencia se puede aproximar utilizando precios diferenciales, y de hecho, ser un resultado natural de la conducta con fines de lucro.

Recent advances in information technology have rekindled interest in the efficiency of markets as resource allocation mechanisms. Traditional economic analysis typically examines situations where the prevalent technology involves no economies of scope and constant or decreasing returns to scale. In such industries the conventional wisdom "set prices at marginal cost" is both economically viable and the likely outcome of competitive forces.
However, many important industries involve technologies that exhibit
increasing returns to scale, large fixed and sunk costs, and significant economies of scope. Two important examples of such industries are
telecommunications services and
information services. In each of these cases the relevant technologies involve high fixed costs, significant joint costs and low, or even zero, marginal costs [
1]. Setting prices equal to marginal cost will generally not recoup sufficient revenue to cover the fixed costs and the standard economic recommendation of "price at marginal cost" is not economically viable. Some other mechanism for achieving efficient allocation of resources must be found.
This paper reviews some key points about how prices should be set in environments of this sort. I examine this question both from a positive and normative point of view. On the normative side I examine characteristics of efficient pricing; on the positive side, I examine the likely outcome of profit-seeking behavior in these environments.
The outcome of this investigation is that
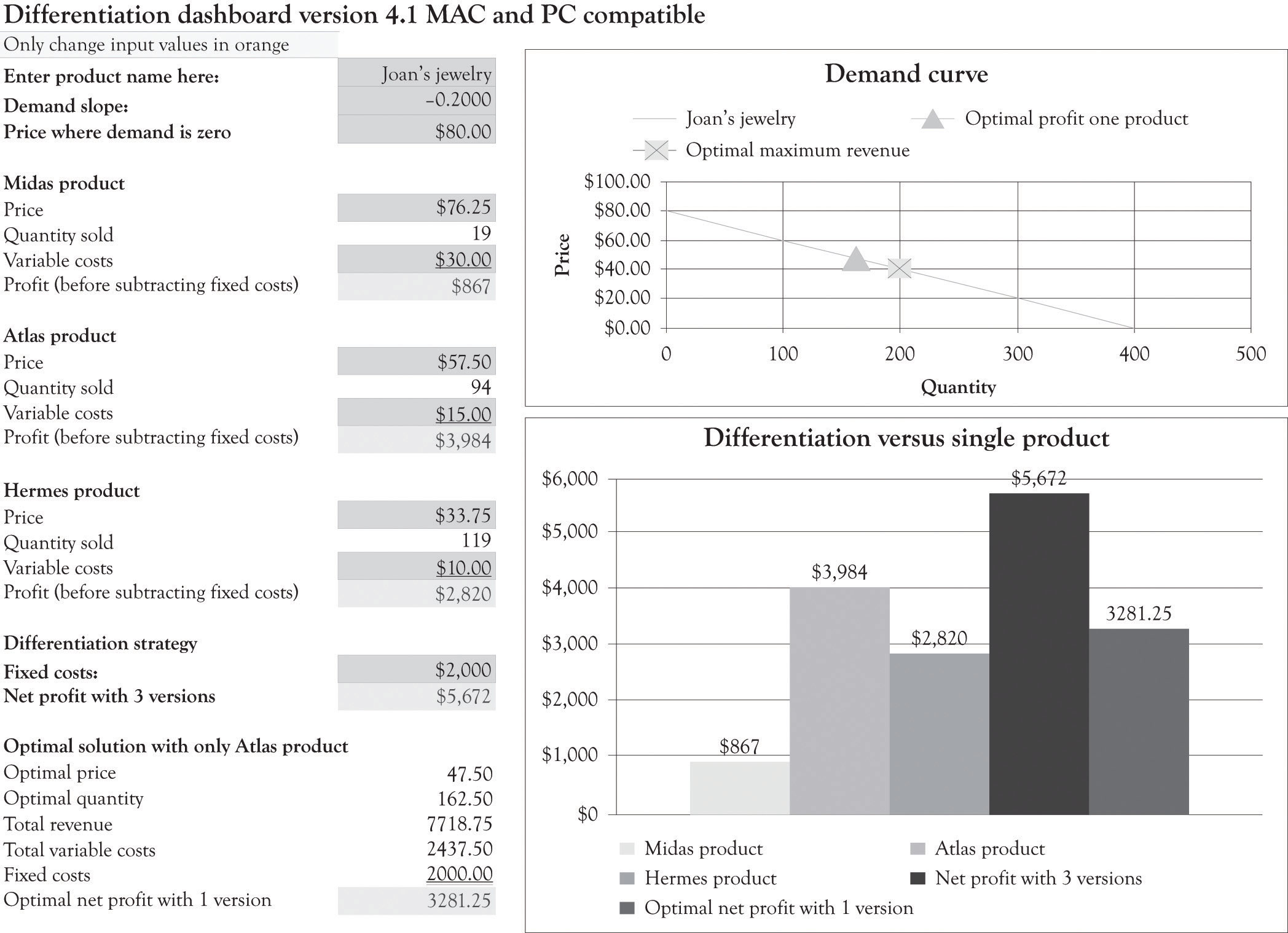
(i) efficient pricing in such environments will typically involve prices that differ across consumers and type of service;
(ii) producers will want to engage in product and service differentiation in order for this differential pricing to be feasible; and,
(iii) differential pricing will arise naturally as a result of profit seeking by firms. It follows that differential pricing can generally be expected to contribute to economic efficiency [
2].

Economists say that an economic situation is
(Pareto) efficient if there is no way to make one consumer better off without making some other consumer worse off. For many cases of interest, Pareto efficient outcomes can be thought of as those that maximize the sum of economic benefits minus costs [
3].
Standard economic analysis can be used to derive the following principle.
Necessary condition for Pareto efficiency. A necessary condition for Pareto efficiency is that that themarginal willingness to pay must equal marginal cost.
In order to correctly understand the concept of efficiency, it is important to be clear about each of the italicized terms in this condition. First "necessary" means that the condition must hold if the situation is economically efficient, but the condition may hold in circumstances without implying that the situation is efficient. For example, forcing a firm to charge a price equal to marginal cost can easily fail to be efficient if such pricing fails to cover total costs; we present several examples of this phenomenon below.
Second, "marginal willingness to pay" refers to the willingness to pay for an incremental unit of the good and "marginal cost" refers to the cost of providing an incremental unit of the good. Once these terms are understood, it is not hard to see why efficiency requires that marginal willingness to pay must equal marginal cost. If any consumer valued an additional unit of the good at more than it cost to produce that unit, then it is possible to make that consumer better off by producing an extra unit of the good and selling it to that consumer at some (consumer-specific) price greater than or equal to the cost of producing the incremental unit. Such a transaction would make the consumer in question better off without making anyone else worse off, showing that the original configuration was not Pareto efficient.
If consumers pay a constant price for each unit of the good that they consume, then it follows that that price must be equal to marginal cost. On the other hand, there is nothing inherent in these principles that says the price must be constant---nonlinear prices are very common in the real world. Efficient pricing only requires that the marginal unit of the good must be sold at marginal cost---not that every unit of the good be sold at marginal cost.
To see this, consider the simple example of a technology of a single-product firm that exhibits constant marginal cost and positive fixed cost. In this case setting price equal to marginal cost is not economically viable since such a price would not recover fixed costs. However, nonlinear pricing may well be viable: for example charging users a positive access fee (to recover the fixed costs) and a constant marginal cost of usage (to recover the variable costs) can easily be efficient in this context.
It should be pointed out that this particular example is very simple. In particular, we have assumed that the firm produces only a single product. If the firm in question produces several products, a more complex analysis is called for. But the central point remains valid: marginal cost pricing does not imply efficiency since there is no guarantee that revenues will be sufficient to cover total costs.

Let us consider this example in more detail. Suppose that there are two classes of consumers for a particular telecommunications service: those with a high willingness to pay and those with a low willingness to pay. The telecommunication service in question exhibits a technology with high fixed costs (of, e.g., building and maintaining a network), but low marginal costs (of, e.g., providing additional service to existing customers).
In this case, the two-part tariff described above is a very natural pricing scheme. Consumers are charged an attachment fee to connect to the network; the revenue from these attachment fees are used to cover the fixed costs of providing the service, while the price of usage itself is pegged to incremental cost. The attachment fee is set so that the firm's total cost is recovered and the necessary condition for Pareto efficiency is satisfied.
It should be emphasized that this is not the only form of efficient pricing in this framework; one could use other forms of nonlinear pricing. The basic requirement that efficiency imposes is the one alluded to above: the marginal willingness to pay must equal marginal cost.

The above analysis, simple though it is, yields an important insight:
The characteristics of consumer demand are an integral part of efficiency judgments. Whether or not a particular policy is efficient cannot be based on cost considerations alone.
Pricing at marginal cost may or may not be efficient: it depends on how the consumers' total willingness-to-pay relates to the total cost of providing the good. To see this, consider the following simple example. Consumer A is willing to pay $10 for a single unit of a good, and consumer B is willing to pay $5. There is a zero marginal cost of producing multiple units of the good, but there is a fixed cost of $10. In this case, total benefits are $15 and total costs are $10, so it is socially worthwhile to produce the good.
There are a variety of ways to recover the fixed cost: each consumer could pay $5, consumer A could pay $10 and consumer B could pay nothing, etc. The only requirement is that consumer A pays no more than $10 and that consumer B pays no more than $5---otherwise they would not be willing to purchase the good.
On the other hand, suppose that the fixed cost of producing the good were $20. In this case, the total benefits from producing the good are $15 and the total costs are $20. There is no way to allocate the good (and the cost of producing it) to the two consumers in a way that makes them both better off than they would be if the good were not produced at all.
This is simply another way of illustrating the point made earlier: efficiency requires that the marginal user face marginal cost, but making all users face a constant price equal to marginal cost can easily fail to be efficient.

The requirement that the marginal user pay marginal cost is a strong one, especially in cases where the marginal cost of usage is close to zero. One prominent example is information goods: the incremental cost of stamping out another CD or printing another book is on the order of a dollar. The incremental cost of downloading a purely digital good, such as a computer program, is on the order of a few cents at most. In these cases, efficient pricing of such goods would require that users with a very low value for such goods pay a very low price.
One might think that it is rare to observe information goods selling for virtually nothing, but on reflection, this is not so uncommon. Many information goods are supported by advertising and sell for prices close to their marginal cost of production and delivery: newspapers and magazines are obvious examples. Books sell for a high price as hardbacks, and much lower prices when reissued as paperbacks. Remaindered books sell for very little. And all sorts of printed material---books, magazines, newspapers, etc.---are available in libraries at effectively zero cost to the users. In addition, there are thousands of shareware computer programs that sell for extremely low prices---on the order of a few dollars.
Similarly, there are telecommunications policies that involve selling services at very low prices. Lifeline rates are a good example. With such plans, needy consumers (who are likely to have a low willingness to pay) can receive telephone services for only a few dollars per month.
Still, a few dollars is still more than a marginal cost of zero. One may well ask how significant a violation of efficiency is involved when marginal users facing a price that is slightly above marginal cost. This question can be answered using the tool of consumer surplus. Consider Figure 1, which illustrates a demand curve for a good; we assume a marginal cost of production of zero. We imagine a nonlinear pricing scheme which collects different fees from different users; we've also illustrated the revenue collected from the consumers in the diagram.
 Figure 1: Efficiency loss.
Figure 1: Efficiency loss.
The black triangle illustrates the efficiency loss from non-marginal cost pricing.
Efficient pricing requires that the marginal user face a marginal price of zero; in the case illustrated, the marginal price is greater than zero, so some users who have positive value for the good choose not to purchase it at that (marginal) price. The aggregate consumers' surplus is less than the maximum possible amount. But how much is this loss? The value of the lost output is simply the area indicated by the black triangle in the diagram: this area the total amount the excluded consumers would have been willing to pay for the good. This triangle represents the value of the transactions that did not take place because the marginal price exceeds marginal cost. However, note that if the marginal price is quite low, the loss from not setting it precisely at zero is also very low. It is at most the marginal price times the number of people who value the good at less than that price. If the marginal price is quite small, the losses from the fact that it exceeds marginal cost will also generally be quite small.

We have seen that efficient pricing requires that the marginal willingness-to-pay equals marginal cost, but that differential and/or nonlinear pricing will typically be required for full efficiency when the underlying technologies have significant fixed costs. We now consider conditions under which profit-seeking firms will have an incentive to price in efficient ways.
The first observation is a simple one: if marginal willingness to pay exceeds marginal cost, there is an obvious incentive for a profit-seeking firm to supply the good at some price between the willingness-to-pay and the marginal cost of provision, thereby increasing its profits. In the extreme case described above, where the marginal cost of provision is zero, a profit-maximizing producer would want to supply the good to everyone who had a positive willingness to pay for the good, no matter how low!
Recall the definition of Pareto efficiency: this is a situation where there is no way to make one person better off without making someone else worse off. If someone values an additional unit of a good at more than its marginal cost, this is inefficient. But this is also a profit opportunity: a producer would find it profitable to provide an incremental unit of the good to anyone who valued it at more than its marginal cost. Thus, the profit motive tends to correct an inefficiency of this sort.
What is it that stands in the way of such mutual Pareto improvements? The problem is that the firm would not want to offer the good at a low price to marginal customers when such an offering would have an adverse effect on the firm's ability to sell to inframarginal customers. That is, selling an incremental unit at more than marginal cost increases profits in the first instance. It is is only when such a sale reduces profits made on the units sold to other consumers, that the firm may wish to forgo this profit opportunity.
To understand this point more deeply let us review the basic microeconomics of price differentiation. Economists generally follow the taxonomy of Pigou, who used the term
price discrimination to describe what we have been referring to as
differential pricing. Pigou described three different forms of price differentiation [
4]:
- First-degree price discrimination means that the producer sells different units of output for different prices and these prices may differ from person to person. This is sometimes known as the case of perfect price discrimination.
- Second-degree price discrimination means that the producer sells different units of output for different prices, but every individual who buys the same amount of the good pays the same price. Thus prices depend on the amount of the good purchased, but not on who does the purchasing. A common example of this sort of pricing is volume discounts.
- Third-degree price discrimination occurs when the producer sells output to different people for different prices, but every unit of output sold to a given person sells for the same price. This is the most common form of price discrimination, and examples include senior citizens' discounts, student discounts, and so on.
 Under first-degree price discrimination, or perfect price discrimination, each unit of the good is sold to the individual who values it most highly, at the maximum price that this individual is willing to pay for it. If the producer has sufficient information to determine the maximum willingness to pay for each consumer, it will be able to extract the entire consumer surplus from the market.
Under first-degree price discrimination, or perfect price discrimination, each unit of the good is sold to the individual who values it most highly, at the maximum price that this individual is willing to pay for it. If the producer has sufficient information to determine the maximum willingness to pay for each consumer, it will be able to extract the entire consumer surplus from the market.
Since the producer gets all the surplus in the market, it wants to make sure that the surplus is as large as possible. Put another way, the producer's goal is to maximize its profits (producer's surplus) subject to the constraint that the consumers are just willing to purchase the amount of the good or service it provides. This means that the outcome will be Pareto efficient, since there will be no way to make both the consumers and the producer better off: the producer's profit can't be increased, since it is already the maximal possible profit, and the consumers' surplus can't be increased without reducing the profit of the producer.
This, in turn, implies that a perfectly price-discriminating producer must produce at an output level where marginal willingness to pay equals marginal cost: if the marginal willingness to pay were greater than marginal cost, that would mean that there is someone who is willing to pay more than it costs to produce an extra unit of output. So why not produce that extra unit and sell it to that person at his or her reservation price, and thus increase profits?
Just as in the case of a competitive market, the sum of producer's and consumers' surpluses is maximized. However, in the case of perfect price discrimination the producer ends up getting all the surplus generated in the market.
Perfect price discrimination is an idealized concept; in order to engage in perfect price discrimination a producer must know the willingnesses-to-pay of its customers and be able to prevent resale. Both of these requirements are difficult to realize in practice and perfect price discrimination is not commonly observed in the real world. However, a close variant---second-degree price discrimination---is quite common.

It is important to understand the sense in which the producer who engages in first-degree price discrimination "extracts all the consumers' surplus" in the market. This is to be interpreted as the surplus
above and beyond the surplus that would accrue to the consumer if he or she had not participated in the market for this particular good or service. Even though consumers acquires no surplus in the particular market in question, they still be substantially better off that if they had not purchased the good at all.
To illustrate this point, let suppose that there are two consumers, A and B who are currently using a pay phone at the local grocery store. They each value this pay-phone service at $10 per month, and it costs them $8 per month to use it. Hence, the consumers each achieve a net surplus of $2 each.
Consumer A would be willing to pay up to $5 additional dollars per month for in-home service, while consumer B would be willing to pay up to $2 additional dollars per month for in-home service. Thus A's total value for in-home service is $15 (=10+5) and B's total value is $12 (=10+2). Suppose that it would cost $21 per month altogether to provide both of these consumers with in-home service.
If the telecommunications provider charged a price of $12 to each consumer for in-home service, consumer B would get zero surplus by purchasing in-house service, but $2 of surplus from using the pay phone. Hence he would continue to use the pay phone. Consumer A would get $3 = 15 - 12 of surplus from in-home service and $2 from the pay phone. Hence consumer A would choose in-home service. Unfortunatly, the $12 of revenue from this consumer would not be sufficient to cover the total costs of $21.
If the provider charged $10 per month, both consumers would purchase in-home service, but again the revenue raised would not succeed in covering the cost of providing that service.
However, if the provider charged user A $13 and user B $10, it would raise a revenue of $23, which would more than cover its costs of $21. Each consumer would get a surplus of $2, the difference between the total value of the service purchased, and how much he or she has to pay for it. Since the consumers would achieve the same surplus from in-home service as from the pay phone, they would be willing to purchase the in-home service at these prices.
In this case, the producer cannot extract the full surplus of consuming the service since there is a competititive alternative yielding a net surplus of $2. As always the pricing flexibility of the producer is limited by the competitive alternatives available. A perfectly price discriminating producer can only extract the surplus above that surplus provided by alternative suppliers. The surplus achievable via the competitive alternative puts a floor on the surplus the consumer ends up with.
 Second-degree price discrimination
Second-degree price discrimination is also known as the case of
nonlinear pricing, since it means that the price per unit of output is not constant but depends on how much one purchases. This form of price discrimination is commonly used by public utilities; for example, the price per unit of electricity often depends on how much is bought and the price of long-distance telephone service is lowest for the largest buyers. In other industries bulk discounts for large purchases are frequently available.
We saw that in the case of perfect price discrimination, the producer has to know the demand curves of the consumers; that is, the producer has to know the exact willingness to pay of each person. Even if the producer knows something about the statistical distribution of willingness to pay---for example, that college students are willing to pay less than yuppies for movie tickets---it might be hard to tell a yuppie from a college student when they are standing in line at the ticket booth.
Similarly, an airline ticket agent may know that business travelers are willing to pay more than tourists for their airplane tickets, but it is often difficult to tell whether a particular person is a business traveler or a tourist.
One way to get around this problem is to offer two different price-quantity packages in the market. One package will be targeted toward the high-demand person, the other package toward the low-demand person. It can often happen that the producer can construct price-quantity packages that will induce the consumers to choose the package meant for them; in economics jargon, the producer constructs price-quantity packages that give the consumers an incentive to self-select.
Under certain assumptions about the form of consumer demand, it can be show that the optimal thing for the producer to do is to offer the consumer with the highest demand an
efficient amount of the good---that is the amount of the good where the willingness to pay for an incremental unit is equal to the incremental cost of providing that unit. The consumer with the lower demand is offered an
inefficient amount of the good---he would be willing to pay more than the incremental cost for an additional unit of the good. The reason that the low-demand consumer is offered an inefficient amount of the good is to avoid making a price-quanitity combination that is too attractive to the consumer with high willingness to pay [
5].
In practice, the producer often encourages this self-selection not by adjusting the quantity of the good, as in this example, but rather by adjusting the quality of the good. The earlier allusion to airline pricing provides a nice example. U.S. airlines normally offer two kinds of airline tickets. One kind has no restrictions: business travelers find these unrestricted fares attractive since their travel plans may change suddenly. The other fare involves several restrictions: the traveler must stay over a Saturday night, must buy the ticket 14 days in advance, and so on. The presence of these restrictions makes the ticket less attractive to business travelers---the travelers with high willingness to pay---but the restrictions are still acceptable to tourists. By and large, each type of traveler selects the fare class intended for him or her and the airline makes substantially more surplus than if it had to sell each ticket at a flat price.

We have seen that if a producer can
identify users with different willingesses-to-pay, and charge them accordingly, there may be no efficiency loss at all: the producer would simply charge each user his or her maximum willingess to pay. Users with high willingnesses-to-pay would pay a high price; users with low willingness-to-pay would pay a low price, but everyone who valued the good at more than its marginal cost of production would be served.
If the producer cannot precisely identify the users, it may want to adjust the characteristics of the good being sold so that users self-select the product targeted for them. In this case, the resulting outcome may be less efficient than it would be if perfect price discrimination were possible. The efficiency cost is the value of the transactions that consumer A would like to consume, but is prevented from doing so by the producer since that would make too attractive a package for consumer B.
In the case of the airline example, this efficiency loss is the extra hassle of buying tickets 14 days in advance, staying over a Saturday night, etc. These sort of restrictions are of little direct benefit to the airline---their only purpose is to separate the low willingess-to-pay consumers from the high willingess-to-pay consumers.
Still second-degree price discrimination may well be more efficient than no price discrimation at all, since without such price discrimination the markets with low demand may not get served at all. Reducing the quality or quantity of the good offered to the market with the low willingness to pay may make them somewhat worse off due to the inconvenience cost. On the other hand, without such a device to segment the market, the producer may not want to servce the low-demand market.
The Saturday-night stay over is a small inconvenience for the tourist traveller, but a large inconvenience for the business traveller. If the airlines were not allowed to differentially price in this way, airline tickes would almost certainly be significantly larger, airline travel would be reduced, and welfare would likely be lower. This point is explored in detail in Deneckere and McAfee
[1996], who show that price/quality discrimination of the sort described can easily make all parties to the transaction better off than if price discrimination were not possible.

In third-degree price discrimination, the producer is able to identify different consumer groups who have different willingnesses to pay. This is a very common form of price discrimination: senior citizen discounts, student discounts, etc. are widely used. This form of price differentiation is often used in telecommunications industries: lifeline pricing, differential pricing for business and households, etc.
Is third-degree price discrimination generally a good thing or a bad thing? One way to answer this question is whether the presence of third-degree price discrimination increases or decreases total surplus. This question was first analyzed by Robinson [
1933]; notable subsequent contributions were made by Schmalensee [
1981], Varian [
1985], and Schwartz [
1990].
For simplicity we will assume that the good is provided at constant marginal cost, and that there are only two groups of consumers involved. We want to compare two scenarios: one where differential pricing is allowed, the other where it is not.
If differential pricing is not allowed the firm is required to sell to the two different groups at the same flat price p
0. If differential pricing is allowed, the firm may charge two different prices to the two groups, p
1and p
2. It can be shown that the change in total welfare (consumer plus producer surplus, denoted by
DW, that results from moving from uniform pricing to differentiated pricing is bounded by the following expression [
6]:
(p0-c) [Dx1 + Dx2] > DW > (p1-c)Dx1 + (p2-c)Dx2
In this expression, Dx1 denotes the change in the demand for the good in market 1.
Some intuition for this expression may be found by examining Figure 2, which depicts the impact of a price change for a single good. The change in welfare from moving from p0 to p1 is given by the trapezoidal area. It is easily seen that this is bounded by the two rectanges (p1-c)Dx1 and (p2-c)Dx2. The complete analysis alluded to above shows that this same bound holds if there are many goods.
 Figure 2: Welfare bounds.
Figure 2: Welfare bounds. The trapezoid is the true change in consumer's surplus. It is bounded above and below by the two rectangles.
This bound has the following implication: the left-hand side of expression (1) shows that a necessarycondition for efficiency to increase when price differentiation is implemented is that total output increases. If output remains constant or decreases when price discrimination is allowed, total welfare must necessarily decline.
On the other hand, welfare may easily increase when price differentiation is allowed, as long as output increases significantly. The requirement is that the weighted change in output on the right-hand side of expression (1) is positive.
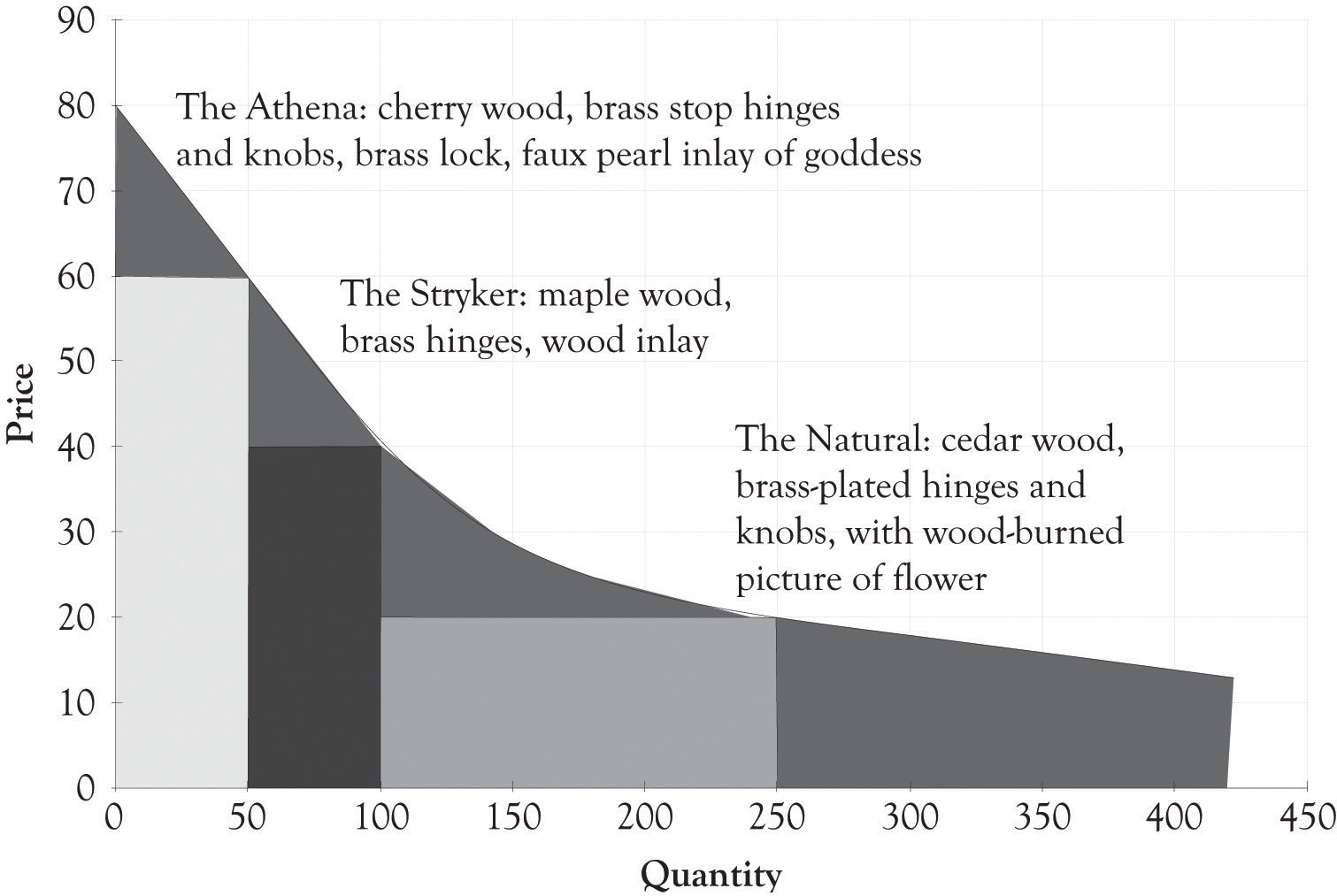
We can see how this works in Figure 3. Here we have illustrated two demand curves. Consumers in market 1 have a high willingness to pay, and consumers in market 2 have a low willingness to pay. If only uniform pricing is allowed, market 2 will not be served. However, if differential pricing is allowed, the firm will find it profitable to serve both markets.
 Figure 3: Unserved markets.
Figure 3: Unserved markets. Without price discrimination, small niche markets may not be served.
This is a good example to keep in mind. Small, niche markets will generally not be well-served if the producer is required to charge a uniform price. In cases of this sort, differential pricing can provide very significant efficiency gains since it allows markets to be served that would otherwise not be served at all. Hausman and MacKie-Mason [
1988] examine this point in some detail and describe some specific examples where it is relevant.

Summing up our discussion of the welfare effects of price discrimination, we see that:
- First-degree price discrimination yields a fully efficient outcome, in the sense of maximizing consumer plus producer surplus.
- Second-degree price discrimination generally provides an efficient amount of the good to the largest consumers, but smaller consumers may receive inefficiently low amounts. Nevertheless, they will be better off than if they did not participate in the market. If differential pricing is not allowed, groups with small willingness to pay may not be served at all.
- Third-degree price discrimination increases welfare when it encourages a sufficiently large increase in output. If output doesn't increase, total welfare will fall. As in the case of second-degree price discrimination, third-degree price discrimination is a good thing for niche markets that would not otherwise be served under a uniform pricing policy.
The general impression that follows from this discussion is if price differentiation allows more consumers to be served it will generally increase welfare. Volume discounts, for example, can be expected to generally enhance welfare. Market segmentation that allows markets to be served that would otherwise be neglected is also a case where overall welfare can be expected to be enhanced.
On the other hand, price differentiation that merely shuffles prices paid by pre-existing customer groups and that does not result in an increase in the number of customers served, or the amount that they consume, will tend to reduce overall welfare. The key issue is whether the output of goods and services is increased or decreased by differential pricing.

We have examined the theory of differential pricing, but what about the facts? The evidence shows that differential pricing is ubiquitous in industries that exhibit large fixed or shared costs. This is true for industries that are highly concentrated
and industries that are highly competitive.
- Airlines The airline industry is highly competitive in many ways, yet it is common to see differential pricing practiced in a variety of forms. As we have seen airlines offer different types of consumers different fares (senior citizen discounts, major corporations, convention goers, etc.); they offer different classes of service (first class, business class, tourist class); they offer different sorts of restricted fares (advanced purchase, Saturday night stayovers, etc.)
- Telecommunications The long-distance telecommunications market in the U.S. involves many different forms of differential pricing. Firms give quantity discounts to both large and small customers; charge business and individuals different rates; and offer calling plans that offer discounted rates based on individual characteristics and usage patterns.
- Publishing A book which sells for $40 can be produced at a marginal cost of $2. This gap between price and marginal cost has led to a variety of forms of differential pricing. Book clubs, hardcover and paperback editions, and remaindered books are all examples of the ways that the product characteristics and adjusted to support differential pricing.
- Lighthouses This example is rather interesting from a historial perspective. Economists have often used lighthouses as an example of a good that would be best provided as a public utility due to the difficulty of recovering costs. For our purposes, their interesting feature is that the cost of servicing incremental users is negligable. As Samuelson [1964] puts it "... it costs society zero extra costs to let one extra ship use the service; hence any ships discouraged from those waters ... will represent a social economic loss ... ." Coase [1974] examined historial record and found that privately financed lighthouses were provided in England for hundreds of years. Even more remarkably, the pricing arrangement they used was quite efficient: they charged on a sliding scale based on the number of voyages a trip took per year. After 6-10 trips per year, the incremental price for the services of the lighthouse was zero, just as efficiency requires.

It is easy to construct examples where some consumers will not be served unless differential pricing is permitted; we have alluded to this in our discussion of "niche markets" earlier. Consider, for example a case with two consumers one of whom would pay $20 for a telecommunications service, and the other of whom would pay $5. For simplicity, assume that the marginal cost of providing the service is zero. If the firm supplying the service is required to sell at a uniform rate to both consumers, it would clearly find it most profitable to set a rate of $20.
If, however, the firm is able to price the product differently to both classes of consumers, it would find it most profitable to sell to the high-value user at a price of $20 and the low-value user at a price of $5.
This is yet another example of how flat pricing may have perverse consquences: forcing a producer to sell to everyone at the same price may sound like a good idea. But it can easily end up encouraging the producer to sell only to the high end of the market. Differential pricing gives the producer an incentive to supply the product to everyone who is willing to pay the incremental cost of production.
An even more striking example can be constructed if we assume that there is also a fixed cost of production of $25. In this case, there is no uniform price at which the firm can recover its costs. The only economically viable solution is for the firm to charge each user according to his or her willingness to pay. If there are large fixed costs, and low marginal costs, differential pricing may be required for a producer to be economically viable.

It is sometimes argued that "essential services" should not be differentially priced. The term "essential service" is rather vague, but one might define it as a service that everyone would want to have if they could afford to purchase it. For such services, differences in willingness to pay arise primarily from differences in income rather than tastes.
If this is the appropriate definition of "essential service" then the case for differential pricing outlined above is even stronger. Differential pricing implies that users with higher willingness-to-pay end up paying higher prices than users with lower willngnesses-to-pay. If differences in willingness-to-pay are primarily determined by differences in income, then differential pricing is effectively charging users with higher income more than those with lower income.

We have considered differential pricing in consumer goods. However, the same principles apply to markets for intermediate goods. In particular, technologies with large fixed costs, low marginal costs and/or significant shared costs may easily require differential pricing to be economically viable.
Consider, for example, the following simple numerical example. A supplier offers a service that has fixed costs of $10 and marginal costs of $1 per unit supplied. Two customers each want to purchase one unit of the service, which they use as an intermediate good to produce a final service which they sell to the consumers. Customer A is willing to pay $12 for the service; customer B is willing to pay $5. Consider the following scenarios.
- Sell service at marginal cost. In this case the producer sells the service at a price of $1 to each of the customers, but would then fail to recover its fixed costs, which is not economically viable.
- Sell service at a flat price. In this case the supplier would find it most profitable to set a price of $12 and sell only to customer A. Customer B would not be able to purchase the service event though it would be willing to cover marginal cost.
- Differential pricing. If differential pricing is feasible, the producer would set a price of $12 for customer A and $5 for customer B. Each customer would be serviced and the supplier would be able to cover its fixed costs.
 Telecommunications services often involve large fixed costs, low marginal costs, and significant shared costs. If such services are required to be provided to a large number of diverse users, and costs are to be covered without the use of externally provided subsidies, it is very likely that differential pricing will be necessary.
Telecommunications services often involve large fixed costs, low marginal costs, and significant shared costs. If such services are required to be provided to a large number of diverse users, and costs are to be covered without the use of externally provided subsidies, it is very likely that differential pricing will be necessary.
To see this, let us consider the simple example used several times before in this paper: a single-product firm with a large fixed cost and a small, constant marginal cost. If a given population is to be served, and flat pricing is the only option, then the price must be set at the willingness to pay of the customer who has the lowest value for the service. If the population has sufficient dispersion in willingness to pay, the person with the lowest value may easily up having a willingness to pay that is less than average cost of production. But if the price is less than the average cost of production, total costs cannot be recovered.
Put another way: the broader the population that must be served, the lower the price that can be charged. But a sufficiently low price can easily result in revenues that are inadequate to recover costs. The only way out of this dilemma is to either provide subsidies for customers with low ability to pay, or for the firm to engage in differential pricing.

We have seen that differential pricing is a natural outcome of profit seeking forces and may easily contribute to economic efficiency. Forcing a policy of flat pricing in an industry where it is inappropriate due to the nature of the technology may well have perverse consequences. The key concern in examining the welfare consequences of differential pricing is whether or not such pricing increases or decreases total output.

 Hal R. Varian
Hal R. Varian, School of Information Management and Systems, 102 South Hall, University of California, Berkeley, CA 94720-4700.
Email:
hal@sims.berkeley.edu
URL:
http://sims.berkeley.edu/~hal.
Research support from NSF SBR-9320481 and Pacific Telephone is gratefully acknowledged.

1. By "joint costs" I mean the cost of those factors of production that are used to produce more than one output. In the remainder of the paper I generally consider the case of a single-output firm since the points I wish to make are most simply illustrated in that context.
2. Huber [
1993], and no doubt several other observers, have made the same point. The contribution of this article is to lay out the economic theory that supports these conclusions.
3. See Varian [
1992], pp 222-223.
4. The original classification can be found in Pigou [
1920]; the following discussion is drawn from Varian [
1993].
5. See Varian [
1993], pp. 427-431 or Varian [
1992], pp 244-248 for a detailed analysis.
6. See Varian [
1985] or Varian [
1992], pp. 250-253.
 R. Coase, 1974.
R. Coase, 1974.
"The Lighthouse in economics," Journal of Law and Economics, vol. 17, pp. 357-376.
R. Schmalensee, 1981.
"Output and welfare implications of monopolistic third-degree price discrimination," American Economic Review, vol. 71, pp. 242-247.
M. Schwartz, 1990.
"Third-degree price discrimination and output: Generalizing a welfare result," American Economic Review, vol. 80, pp. 1259-1262.
H. R. Varian, 1985.
"Price discrimination and social welfare," American Economic Review, vol. 75, pp. 870-875.
Copyright © 1996, First Monday
Differential Pricing and Efficiency by Hal Varian
First Monday, Volume 1, Number 2 - 5 August 1996
http://firstmonday.org/htbin/cgiwrap/bin/ojs/index.php/fm/article/viewArticle/473/394

.jpg)
